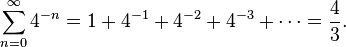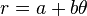Νότα Κυμοθόη"ΑΡΧΙΜΗΔΗΣ"Ιστορική έρευνα

ΝΟΤΑ ΚΥΜΟΘΟΗ:ΑΡΧΙΜΗΔΗΣ
"ΔΩΣΤΕ ΜΟΥ ΕΝΑ ΜΕΡΟΣ ΝΑ ΣΤΑΘΩ ΚΑΙ Θ΄ΑΝΑΠΟΔΟΓΥΡΙΣΩ ΟΛΗ ΤΗ ΓΗ"
Αφορμή τα Φάρσαλα, η αρχαία πόλη, ο χαλβάς και φυσικά οι Πέρσες...

Η πόλη είναι χτισμένη στους πρόποδες ενός λόφου, του Ναρθακίου όρους, με υψόμετρο 160 μέτρα. Αρχαιολογικά ευρήματα μαρτυρούν την αδιάλειπτη κατοίκηση της τοποθεσίας ήδη από την Νεολιθική εποχή. Ακόμη και σήμερα είναι ορατά τα Κυκλώπεια τείχη που προστάτευαν την πόλη. Υπάρχει επίσης και ένας θολωτός τάφος της περιόδου αυτής.

Στα ιστορικά χρόνια, η πόλη είναι γνωστή με το όνομα Φάρσαλος. 

ΑΣ ΔΟΥΜΕ ΤΗΝ ΑΛΗΘΕΙΑ ΠΟΥ ΜΑΣ ΕΧΟΥΝ ΚΡΥΨΕΙ...

Εντύπωση μου κάνει το γεγονός της μεγάλης καταστροφής αυτών των χωρών, όπου κρύβουν στα σπλάγχνα της γης τους ιστορικά στοιχεία Ελλήνων. Εντύπωση μου κάνει που η ελληνική πολιτισμική κοινότητα, συμπεριλαμβανομένου και του Υπουργείου Πολιτισμού και των εκάστοτε Υπουργών του, να είναι τελείως στουρνάρια κι αμόρφωτοι γι΄αυτή τη θέση ενός Υπουργείου που μέχρι τώρα έχει αφήσει την μεγάλη ελληνική κληρονομιά στο έλος του Θεού και των παντός είδους αρπαχτικών. Εντύπωση μου κάνει η συνεχής και προσχεδιασμένη(?????????) αδιαφορία πληρωμένων Κυβερνητικών Ταγών να υπηρετούν τα ελληνικά συμφέροντα και φυσικά τον ελληνικό πολιτισμό, αλλά να μη τον προστατεύουν. (ΑΝ ΤΟΥΣ ΕΚΛΕΒΑΝ ΤΟ ΑΥΤΟΚΙΝΗΤΟ ΤΟΥΣ ή ΤΟ ΣΠΙΤΙ ΤΟΥΣ θα ΑΔΙΑΦΟΡΟΥΣΑΝ ΤΟ ΙΔΙΟ;)

Ας έρθουμε στο προκείμενο:
1. Η λέξη βίβλος είναι γνήσια ελληνική και φυσικά η λέξη Θεός είναι γνήσια ελληνική.

{Η Βύβλος ήταν αρχαία πόλη των Φοινίκων( οι Φοίνικες ήταν Έλληνες προερχόμενοι από την ελληνική πόλη Φοινίκη, βόρεια από τα σημερινά Ιωάννινα της Ηπείρου, δηλαδή στη σημερινή Αλβανία. Σώζονται ερείπια της πόλης) χτισμένη στις ακτές του Λιβάνου. Κατά τους φοινικικούς χρόνους ήταν μεγάλο ναυτιλιακό και εμπορικό κέντρο, κυρίως λόγω της εξαγωγής παπύρου.

Μυθολογία

Σύμφωνα με τον μύθο, η αρχαία αιγυπτιακή θεότητα Ίσιδα (που ήταν ιέρεια στην αρχαία πόλη Βυζάντιο που είχαν ιδρύσει οι Μεγαρείς=σημερινή Κωνσταντινούπολη=ειςτην πόλην=Ιστανμπούλ. και διωγμένη από την ήρα γιατί κοιμήθηκε με το Δία βρέθηκε στην Αίγυπτο)πήγε στη Βύβλο για να βρει τα μέλη του νεκρού συζύγου της Όσιρι. Τα νερά ξέβρασαν το κιβώτιο με τα μέλη του Όσιρι στις ακτές της Φοινίκης, όπου και χώθηκε στη ρίζα ενός δένδρου. Το δένδρο αναπτύχθηκε ταχύτατα και έκρυψε το κιβώτιο στον κορμό του. Όταν όμως το έκοψαν για την υποστύλωση της στέγης του βασιλικού ανακτόρου, το δένδρο άρχισε να διαχέει εξαιρετική ευωδία.

Ακούγοντας η Ίσιδα το γεγονός ταξίδεψε στη Βύβλο. Εκεί μεταμορφωμένη σε βρεφοκόμο, η βασίλισσα της εμπιστεύθηκε την ανατροφή του νεογέννητου γιου της. Η Ίσιδα δέχτηκε και θα έκανε το παιδί αθάνατο, αν η μητέρα του δεν ταραζόταν, όταν είδε τη θεά κάποιο βράδυ να λούζει το παιδί στις καθαρτήριες φλόγες. Για να την καθησυχάσει, η Ίσιδα της αποκάλυψε ποια ήταν και τον λόγο που την έφερε στη Φοινίκη. Ο βασιλέας της παρέδωσε τον πολύτιμο στύλο και η θεά απέσπασε το φέρετρο του συζύγου της, το κατάβρεξε με τα δάκρυά της και το μετέφερε στην Αίγυπτο. Εκεί το έκρυψε στα έλη της Βουτούς, μακριά από το μίσος του Σετ.

Με το πέρασμα των χρόνων ο πάπυρος ονομάστηκε βιβλίο, από την ελληνική γλώσσα, διότι η περιοχή ήταν ελληνική...αλλά υπάρχουν κι αποδείξεις...

Πάπυρος του Δερβενίου

Φωτογραφική ανατύπωση του Παπύρου

Ο Πάπυρος του Δερβενίου είναι αρχαίο ελληνικόχειρόγραφο και ένα από τα αρχαιότερα γνωστά φιλολογικά έγγραφα της Ευρώπης. Χρονολογείται στο δεύτερο ήμισυ του 5ου αιώνα π.Χ.. Βρέθηκε το 1962 στον τάφο ενός ευγενούς στο Δερβένι. Αρχικά το κείμενο έμεινε αμετάφραστο, ώσπου τον Οκτώβριο του 2006, ο Έλληνας καθηγητής κλασσικής φιλολογίας της Φιλοσοφικής Σχολής του ΑΠΘ και παπυρολόγος Κυριάκος Τσαντσάνογλου ανακοίνωσε την επιτυχή πλήρη μετάφραση του κειμένου. Περιέχει την φιλοσοφική έκθεση ενός άγνωστου συγγραφέα περί της γεννήσεως των θεών. Πιστεύεται ότι ο συγγραφέας ανήκε στο περιβάλλον του Αναξαγόρα. Ο πάπυρος φυλάσσεται στο Αρχαιολογικό Μουσείο Θεσσαλονίκης.

Έτσι απλά για να λυθεί η κάθε πλάνη, σχετικά με την ονομασία Βίβλος και βιβλική εποχή.
ΑΦΟΡΑ ΚΑΘΑΡΑ ΤΗΝ ΕΛΛΗΝΙΚΗ ΕΠΟΧΗ όπου ΕΜΠΟΡΕΎΟΝΤΑΝ ΤΟΝ ΠΑΠΥΡΟ, ΓΙΑΥΤΟ ΚΑΙ ΟΙ ΑΡΧΑΙΟΙ ΕΛΛΗΝΕΣ ΕΓΡΑΦΑΝ ΣΕ ΠΑΠΥΡΟΥΣ
(Κάηκε η βιβλιοθήκη της Αλεξάνδρειας; Καταστράφηκαν όλοι οι πάπυροι; Τότε πως σώθηκαν τα αρχαία ελληνικά κείμενα;)

Περί το 600 π.Χ. σε μια πλίθινη επιγραφή που ονομάζεται

τετραγράμματον εικάζουν πως βρέθηκε χαραγμένο το όνομα του Θεού. Αυτό όμως είναι το όνομα ενός Θεού της περιοχής εκείνης. Ονόματα Θεών υπάρχουν πολλά...Αυτό δεν αποτελεί εύρημα για την αρχή της γραφής, διότι η πιο αρχαία γραφή είναι στο Δισπυλιό και φυσικά έχουμε και τα ευρήματα από το Σπήλαιο Πλάγθι των Θηβών 12.000π.Χ για τα οποία δεν γίνεται πουθενά λόγος.
ΑΙΣΧΟΣ ΔΗΛΑΔΗ!..
(ΑΛΛΑ ΤΟ ΠΙΟ ΜΕΓΑΛΟ ΑΙΣΧΟΣ ΕΙΝΑΙ ΤΟ ΟΤΙ ΘΕΛΟΥΝ ΤΟΥΣ ΦΟΙΝΙΚΕΣ ΝΑ ΜΗΝ ΕΙΝΑΙ ΕΛΛΗΝΕΣ!..)

Αλλά η ονομασία ΤΕΤΡΑΓΡΑΜΜΑΤΟΝ  είναι γνήσια ελληνική. ΝΑ ΘΥΜΗΣΩ ΑΠΛΑ πως ο Χριστός, το όνομά του ήταν ΕΜΜΑΝΟΥΗΛ κι αργότερα οι ΈΛληνες του έδωσαν το όνομα Ιησούς Χριστός, τόνιζε κι έλεγε: "ΕΓΩ ΕΙΜΙ ΤΟ ΑΛΦΑ ΚΑΙ ΤΟ ΩΜΕΓΑ" εννοώντας φυσικά όλα τα ονόματα των ΘΕΩΝ από το Α έως το Ωμέγα που μέχρι τότε υπήρχαν. Τώρα αν ο Εμμανουήλ ήταν Έλληνας στην καταγωγή του, ας το εξετάσουμε σε μια άλλη έρευνα...

Οι Έλληνες-ευρήματα κι επιγραφές έχουμε πριν πολλά χιλιάδες χρόνια για τους Θεούς τους-από αυτή την επιγραφή... Τι μας έχουν κρύψει λοιπόν; Και γιατί σχετίστηκαν όλα με τους παπύρους; Αφού όλοι σε παπύρους έγραφαν. Και τα κείμενα των αρχαίων ΕΛλήνων σοφών σε παπύρους ήταν. Μπορεί να μας πει το ΒΑΤΙΚΑΝΟ πόσους ελληνικούς παπύρους=βιβλία αρχαίων Ελλήνων έχει στα υπόγεια του Μουσείου Βατικανού;
Βιβλική λοιπόν εποχή, είναι η εποχή όπου έχουμε γραφτά μνημεία σε παπύρους και τα πρώτα μνημεία είναι των αρχαίων ΕΛλήνων Σοφών και ιερέων, διότι τα ιερά Λούξορ και Καρνάκ ήταν Ελλήνων Θεών, Άμωνος ΔΙός.

Ας πάμε λοιπόν στην εποχή του μεγάλου κατακλυσμού που δεν έγινε σε μια μέρα, αλλά σιγά-σιγά.
Οι άνθρωποι μετακινήθηκαν και μαζί με αυτούς και τα ζώα τους δηλαδή τα κοπάδια τους. Νομάδες λοιπόν μετακινούμενοι, περαστικοί, δηλαδή...ΕΒΡΑΙΟΙ...


ΔΑ ΠΑΜΕ ΝΑ ΔΟΥΜΕ ΛΙΓΟ ΤΗΝ ΚΑΤΑΓΩΓΗ ΤΩΝ ΦΟΙΝΙΚΩΝ
ΠΟΥ ΗΤΑΝ ΓΝΗΣΙΑ ΕΛΛΗΝΙΚΑ ΦΥΛΑ ΣΤΗ ΒΟΡΕΙΟ ΗΠΕΙΡΟ
ΚΑΙ ΝΑ ΔΟΥΜΕ ΚΑΙ ΝΑ ΣΚΕΦΤΟΥΜΕ ΠΩΣ ΤΗΝ ΚΑΤΕΣΤΡΕΨΑΝ...


Ιστορία της Ηπείρου
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Προϊστορία και ιδρυτικοί μύθοι

Η Ήπειρος στην Αρχαιότητα

Ελληνικές περιοχές της Ηπείρου τον 5ο - 6ο αιώνα π.Χ.

Από τη δεύτερη χιλιετία προ Χριστού ζούσαν διάφορα ελληνικά (ηπειρώτικα) φύλα, τα κυριότερα ήταν οιΘεσπρωτοί, οι Χάονες, οι Μολοσσοί. Ιδιαίτερα, η περιοχή που εκτείνεται από τις ακτές της Αδριατικής, περιλαμβάνοντας τις περιοχές του Ογχησμού (σημερινών Αγίων Σαράντα) και Βουθρωτού ως την λίμνηΑχρίδα στην ενδοχώρα, κατοικούνταν από τους Χάονες (Χαονία).

Με την περιοχή σχετίζονται διάφορες αφηγήσεις που ανάγονται στον τρωικό επικό κύκλο: ο Ελπήνωρ, μετά τον Τρωικό πόλεμο, επικεφαλής ομάδας Λοκρών και Αβάντων, ιδρύει τις πόλεις Ωρικό και Θρόνιο(στον κόλπο του Αυλώνα). Ο Αιακίδης Νεοπτόλεμος, συνοδευόμενος από Μυρμιδόνες, ίδρυσε την αρχαίαΒυλλίδα (κοντά στην Απολλωνία). Ο Αινείας και ο Έλενος, εγκαταστάθηκαν με μια ομάδα Τρώων στην Χαωνία και ίδρυσαν το Βουθρωτό. Επίσης ένας γιος του Έλενου, ο Χάων υπήρξε ο γενάρχης των Χαόνων.

Αρχαία Εποχή
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Σημαντικοί οικισμοί κατά την αρχαιότητα στην περιοχή υπήρξαν εκτός από το Βουθρωτό (απέναντι από την Κέρκυρα), ο Ογχησμός (σύγχρονοι Άγιοι Σαράντα), η Φοινίκη, η Αντιγόνεια (κοντά στο σημερινό Αργυρόκαστρο), η Αντιπάτρεια (σύγχρονο Βεράτι), η Αμαντία, η Νίκαια, το Πήλιον, το Ωρικόν και μικρότεροι οικισμοί ήταν οι Κεμάρες (σύγχρονη Χειμάρρα) και το Θρόνιο.

ΑΡΧΑΙΟ ΕΛΛΗΝΙΚΟ ΘΕΑΤΡΟ ΣΤΗΝ ΑΡΧΑΙΑ ΦΟΙΝΙΚΗ ΤΗΣ ΒΟΡΕΙΟΥ ΗΠΕΙΡΟΥ

Εκτός από τους Χάονες που επιβλήθηκαν σταδιακά στην περιοχή, άλλα ηπειρωτικά φύλλα στην ενδοχώρα υπήρξαν οι Αντιτάνες, οι Παραυοί, οι Πρασαιβοί και πιο βόρεια οι Δεξάροι (ή Δεσσαρήτες).

Κατά το διάστημα 650-500 π.Χ. οι Χάονες επεκτάθηκαν στην ευρύτερη περιοχή, καθώς η δύναμή τους εκτείνονταν στην παραθαλάσσια περιοχή από τον ποταμό Καλαμά ως τον κόλπο του Αυλώνα και στην ενδοχώρα μέχρι τις πεδιάδες της περιοχής της Κορυτσάς. Δεδομένου ότι ο τύμβος ΙΙ στη θέση Κούτσι, κοντά στην Κορυτσά, περιείχε ταφές ηγεμόνων του 7ου αιώνα π.Χ., η αρχή επεκτάσεως των Χαόνων μπορεί να χρονολογηθεί στην εποχή εκείνη^[3].

Κατά την κλασσική εποχή, το 375 π.Χ. όλα τα ηπειρωτικά φύλα ενώθηκαν σε μία πολιτική οντότητα, κάτω από τη δυναστεία του Αιακίδη Αλκέτα (των Μολοσσών) και το 232 π.Χ. εγκαθιδρύεται στην Ήπειρο το αβασίλευτο Κοινό των Ηπειρωτών, με πρωτεύουσα τη Φοινίκη. Ως ενιαίο κράτος η Ήπειρος υπήρξε υπολογίσιμη δύναμη στην ευρύτερη περιοχή μέχρι την ρωμαϊκή κατάκτηση το 167 π.Χ..

Πάμε σε μια αρχαία τοποθεσία που ονομάζεται ΕΛΑΜ στην αρχαία Περσία, της οποίας τα αρχικά είναι: ΕΛ= ΘΕΟΣ και ΑΜ= ελληνική ονομασία αστρονομικής μονάδας μέτρησης απόστασης ήλιου και γης.
ΕΛ= Θεοί, ιερείς του Ήλιου, μάγοι αργότερα
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Πριν όμως θα ξεκαθαρήσουμε ένα θέμα: Οι Πέρσες ήταν ελληνικά φύλα της προ κατακλυσμιαίας περιόδου από τις περιοχές της Αιγαίας Γης. Όσο για τους Εβραίους, το όνομα παραπέμπει σε νομάδες κατοίκους από την περιοχή γύρω από τον ποταμό Έβρο.

ΔΙΑΒΑΣΤΕ ΚΑΙ ΒΓΑΛΤΕ ΜΟΝΟΙ ΣΑΣ ΣΥΜΠΕΡΑΣΜΑΤΑ,..κι επειδή η ΑΛΗΘΕΙΑ ΕΙΝΑΙ ΑΛΗΘΕΙΑ ΚΑΛΟ ΘΑ ΕΙΝΑΙ ΝΑ ΤΗΝ ΜΑΘΟΥΝ ΟΙ ΕΛΛΗΝΕΣ ΠΟΥ ΕΝΔΙΑΦΕΡΟΝΤΑΙ, ΑΛΛΑ ΚΑΙ ή μη Έλληνες.
 Τι θα πει δηλαδή "αρχαία βιβλική χώρα;"

Ελάμ
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Η αρχαία χώρα του Ελάμ στον Περσικό Κ.

Ελαμίτικο ανάγλυφο με μια νεαρή γυναίκα νηματουργό – Μουσείο του Λούβρου

Ελαμίτικο ανάγλυφο που παριστάνει γυναίκα με ουρά ψαριού να κρατάει φίδια – Μουσείο του Λούβρου

Ασημένιο κύπελλο με Ελαμίτικη επιγραφή – 3η χιλιετία π.χ.

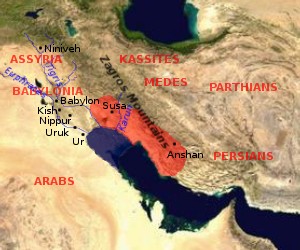
Με την ονομασία Ελάμ φέρεται αρχαία Βιβλική χώρα ανατολικά της Βαβυλώνας, κατά μήκος των ΒΑ. ακτών του Περσικού κόλπου, της οποίας όμως πρωτεύουσα φέρεται η ιστορική πόλη Σούσα, η οποία όταν την κατέλαβαν οι Πέρσες κατέστη πρωτεύουσα της Σατραπείας της Σουσιανής.
Η χώρα Ελάμ προσδιορίζεται στη θέση του σημερινού Χουζιστάν, όπου και η αρχαία Σουσιανή. Πρόκειται για περιοχή της νοτιοδυτικής Περσίας.

Το Ελάμ στη Βίβλο
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Κάτοικοι της χώρας Ελάμ σύμφωνα με την Βίβλο ήταν οι Εβραίοι Ελαμίτες Σημίτες στην καταγωγή απόγονοι του Ελάμ εγγονού του Νώε και μεγαλύτερου γιου του Σημ (Γένεση 10:22, Έσδρας 4:09), με τη Σημιτική καταγωγή των Ελαμιτών δεν συμφωνεί όμως η αρχαιολογική έρευνα.

Γεν. 10,22 : Υιοί του Σημ είναι οι Ελάμ, Ασσούρ, Αρφαξάδ, Λουδ, Αράμ και Καϊνάν.

Αναφέρεται τόσο στην Παλαιά Διαθήκη όσο και στην Καινή Διαθήκη, όταν προσκυνητές Ελαμίτες είχαν προσέλθει στηνΙερουσαλήμ για την εβραϊκή Πεντηκοστή, ή Γιορτή του θερισμού.

Ιστορία του Ελάμ
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Η ιστορία του Ελάμ χωρίζεται σε τρεις περιόδους:

• Η πρωτο – Ελαμίτικη περίοδος (3200 π.Χ. – 2700 π.Χ.)
• Η παλαιά – Ελαμίτικη περίοδος (2700 π.Χ. – 1600 π.Χ.)
• Η μέση – Ελαμίτικη περίοδος (1600 π.Χ. – 1100 π.Χ.)
• Η νέα – Ελαμίτικη περίοδος (1100 π.Χ. – 539 π.Χ.)

Παλαιά Ελαμίτικη περίοδος
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Αναφέρονται τρία προϊστορικά πρωτο – Ελαμίτικα κρατίδια : Ανσάν (σημερινό Φαρσί), Αβάν (σημερινό Λουριστάν) καιΣιμάσχκι (σημερινό Κερμάν), μερικοί μελετητές συμπεραίνουν ότι είναι το ίδιο το Ελάμ σε διαφορετικές χρονικές περιόδους. Ίχνη κατοίκησης στο Ελάμ υπάρχουν από το 7000 π.Χ. η πρωτεύουσα Σούσα ιδρύθηκε γύρω στο 4000 π.Χ. στις όχθες του ποταμού Καρούν, την πρωτο - Ελαμίτικη περίοδο ως το 2700 π.Χ. τα αρχαιολογικά ευρήματα έδειξαν μια ιδιαίτερη μορφή κεραμικής. Η επίθεση των Σουμερίων με τον βασιλιά της Κις Εμμεμπαραγκέσι (2650 π.Χ.) ήταν η αιτία για την έναρξη της παλαιο – Ελαμίτικης περιόδου, η Σουμεριακή κεραμική αντικατέστησε τότε την Ελαμίτικη. Την παλαιά Ελαμίτικη περίοδο δημιουργήθηκε το κράτος του Ελάμ σαν μια προσπάθεια των παλιών κατοίκων της περιοχής να οργανωθούν στρατιωτικά και διοικητικά απέναντι στην κατοχή της χώρας τους από τους Σουμερίους. Τρεις βασιλικές δυναστείες κυριάρχησαν στο Ελάμ την παλαιά περίοδο:

• Η δυναστεία των Αβάν (2400 π.Χ. – 2100 π.Χ.)
• Η δυναστεία των Σιμάς (2100 π.Χ. – 1970 π.Χ.)
• Η δυναστεία των Επαρτί (1970 π.Χ. – 1770 π.Χ.)

Η δυναστεία των Αβάν είναι γνωστή από τις επιγραφές των Ακκάδων την εποχή της κοσμοκρατορίας της δυναστείας του Σαργών του μέγα ο οποίος αφού κατέκτησε τα Σούσα επιχείρησε βίαια να αντικαταστήσει την Ελαμίτικη γλώσσα με την Ακκαδική. Με την κατάρρευση της αυτοκρατορίας των Ακκάδων την εποχή του τρισέγγονου του Σαργών Σαρ – καλί – Σαρί η δυναστεία των Αβάν κήρυξε την ανεξαρτησία του Ελάμ με τον βασιλιά Ινσουσινάκ (2240 π.Χ. – 2220 π.Χ. ). Τα Ακκαδικά αποβλήθηκαν εντελώς από την περιοχή, η δυναστεία των Αβάν κατέρρευσε (2100 π.Χ.) ύστερα από επιδρομές της ληστρικής φυλής των Γκούτι από το βόρειο Ιράν που μιλούσαν συγγενική γλώσσα με τους Ελαμίτες. Έναν αιώνα αργότερα ο βασιλιάςΣουλγκί της 3ης δυναστείας της Ουρ κατέλαβε τα Σούσα αλλά η δύναμη των Σουμερίων ξεκίνησε απότομα να φθίνει. Την εποχή του εγγονού του Σουλγκί Ιμπί-Σιν οι Ελαμίτες κυρίευσαν και λεηλάτησαν την Ουρ ανατρέποντας την τελευταία δυναστεία των Σουμερίων (2004 π.Χ.) ο ίδιος ο Ιμπί Σιν μεταφέρθηκε αιχμάλωτος στα Σούσα με πλήθος από λάφυρα. Η Ακκαδική δυναστεία της Ισίν που αντικατέστησε την 3η δυναστεία της Ουρ έδιωξε τους Ελαμίτες από την Μεσοποταμία επιστρέφοντας τα κλοπιμαία από τα Σούσα όπως το άγαλμα του θεού Νάννα. Η δυναστεία των Επαρτί συνέπεσε με την άνοδο της δυναστείας των Αμορριτών στην Βαβυλώνα, η δυναστεία ανατράπηκε από τον Χαμουραμπί που κατέλαβε ολόκληρη την Μεσοποταμία.

Μέση Ελαμίτικη περίοδος
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Η μέση – Ελαμίτικη περίοδος ξεκινά με την άνοδο της δυναστείας των Ανσανιτών (1500 π.Χ.) οι οποίοι έφεραν πλήρη εξελαμιτισμό των Σούσων παίρνοντας τον τίτλο του ‘βασιλιά του Ανσνάν και των Σούσων’. Προηγήθηκαν πέντε βασιλείς των Κυδινουιδών (1500 π.Χ. – 1400 π.Χ.) οι οποίοι εξακολουθούσαν να χρησιμοποιούν την Ακκαδική γλώσσα, αλλά οι διάδοχοι τους Ιγκεχαλκίδες (1400 π.Χ. – 1210 π.Χ.) και Σουτρουκίδες (1210 π.Χ. – 1100 π.Χ.) χρησιμοποιούν τα Ελαμίτικα. Από τους Ιγκεχαλκίδες είναι γνωστοί 10 βασιλείς πολλοί από αυτούς παντρεύτηκαν πριγκίπισσες των Κασσιτών οι οποίοι σποραδικά είχαν καταλάβει το Ελάμ (1320, 1230 π.χ.) τότε καθιερώθηκαν οι Ελαμίτικες θεότητες στα Σούσα. Με τους Σουτρουκίδες η Ελαμίτικη αυτοκρατορία έφτασε στο αποκορύφωμα της δόξας της, ο βασιλιάς Σουτρούκ Νακχουντέ και οι τρεις γιοί του έκαναν σκληρές επιθέσεις στην Βαβυλώνα που βρισκόταν υπό την εξουσία των Κασσιτών. Δημιούργησαν ισχυρό στρατό, έκτισαν λαμπρά κτίρια και ναούς, ο Σουτρούκ Νακχουντέ λεηλάτησε την Βαβυλώνα μεταφέροντας στα Σούσα πολλά πολύτιμα κλοπιμαία όπως το άγαλμα του Μαρδούκ από τον ναό της Εσαγκίλα και την στήλη του Χαμουραμπί. Ανέτρεψε τον Κασσίτη βασιλιά της Βαβυλώνας Ζαμπαμπα – σουμά – ιντίν αντικαθιστώντας τον με τον γιο του Κουτίρ – Νακχουντέ ύστερα από αυτόν οι Κασσίτες ανατράπηκαν στην Βαβυλώνα από μια τοπική δυναστεία της Ισίν την 5η δυναστεία της Βαβυλώνας. Ο βασιλιάς της 5ης δυναστείας Ναβουχοδονόσορ Α΄ ελευθέρωσε ολοκληρωτικά την Βαβυλώνα από τους Ελαμίτες, λεηλάτησε τα Σούσαμεταφέροντας πίσω τα πολύτιμα κλοπιμαία όπως το άγαλμα του Μαρδούκ και την στήλη του Χαμουραμπί. Για την επόμενη περίοδο δεν υπάρχουν επαρκή στοιχεία, αυτό που παρατηρούμε είναι συμμαχίες του Ελάμ με την Βαβυλώνα για να αντιμετωπιστεί η υπερδύναμη της Ασσυρίας, ένας βασιλιάς της Βαβυλώνας ο Μαρ μπιτί απλά ουσούρ ήταν Ελαμίτικης καταγωγής.

Νέα Ελαμίτικη περίοδος
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Την νέα – Ελαμίτικη περίοδο παρατηρούμε την ύπαρξη ενός λαού στα οροπέδια του Ιράν που μιλούσε την Ινδο – Ευρωπαική γλώσσα, οι Ασσυριακές πηγές από το 800 π.Χ. μιλούσαν για τους ‘ισχυρούς Μήδες’ . Ανάμεσα στις υπόλοιπες φυλές των Μήδων ήταν η φυλή των Παρσί στις όχθες της λίμνης Ουρμιά, καταγράφονται για πρώτη φορά το 844 π.Χ. τον 7ο αιώνα π.χ. ήταν υποτελείς των Ασσυρίων. Συμμάχησαν με τον σφετεριστή βασιλιά της Βαβυλώνας Μαρδούκ απλά Ιντινά Β' στην επανάσταση του εναντίον του βασιλιά της Ασσυρίας Σαργών Β΄ (722 π.Χ.), σύμμαχοι του Μαρδούκ απλά Ιντινά Β' ως την εποχή που η Βαβυλώνα ανακατελήφθη από τον Σαργών (710 π.Χ.). Ο γιος του Σαργών Σενναχειρείμ συνέτριψε οριστικά τον Μαρδούκ απλά Ιντινά Β' (702 π.Χ.) ο ίδιος ο σφετεριστής Χαλδαίος βασιλιάς κατέφυγε στο Ελάμ όπου παρέμεινε επικηρυγμένος από τον Ασσύριο βασιλιά ως τον θάνατο του. Οι Ελαμίτες κατέλαβαν την Βαβυλώνα (694 π.Χ.) δολοφονώντας τον βασιλιά Ασούρ ναδίν σουμί γιό του Σεναχειρίμπ που είχε τοποθετηθεί στην θέση αυτή από τον πατέρα του, τοποθέτησαν βασιλιά τον Νεργκάλ ουσεζίμπ που αιχμαλωτίστηκε την επόμενη χρονιά από τους Ασσύριους. Οι Ελαμίτες τοποθέτησαν στην συνέχεια βασιλιά τον Χαλδαίο πρίγκιπα Μουσεζίμπ Μαρδούκ, παρέμεινε ως την χρονιά που ο Σενναχειρείμ κατέλαβε και ισοπέδωσε την Βαβυλώνα για να εκδικηθεί τον θάνατο του γιου του (689 π.Χ.). Οι σχέσεις των Ελαμιτών με τους Ασσύριους βελτιώθηκαν μονάχα ένα διάστημα την εποχή του βασιλιά Ουρτακού όταν ήταν βασιλιάς της Ασσυρίας ο Σαρδανάπαλος αλλά τελικά βρήκε και αυτός τον θάνατο από τους Ασσυρίους (665 π.Χ.). Οι εμφύλιες διαμάχες στην συνέχεια εξασθένησαν την χώρα,κάθε βασιλιάς έμενε στον θρόνο ελάχιστα ο Σαρδανάπαλος βρήκε την ευκαιρία να καταλάβει και να ισοπεδώσει ταΣούσα που έγιναν Ασσυριακή επαρχία (640 π.Χ.). Στην περιοχή κυριάρχησαν σύντομα οι Αχαιμενίδες πρόγονοι των Περσών μαζί με τους Μήδους που ζούσαν στην ίδια περιοχή ήταν υποτελείς των Ασσυρίων που εξασθένησαν σημαντικά μετά τον θάνατο του Σαρδανάπαλου. Ο βασιλιάς των Μήδων Κυαξάρης εκμεταλλεύτηκε την αναρχία στην Ασσυρία και ελευθέρωσε το Ελάμ συμμαχώντας με τον Χαλδαίο στρατηγό Ναβοπολάσαρ (616 π.Χ.) τον ιδρυτή της Χαλδαίικης αυτοκρατορίας.

ΠΑΜΕ ΤΩΡΑ ΣΤΟΝ παππού μου τον ΑΡΧΙΜΗΔΗ

Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Ο Αρχιμήδης ο Συρακούσιος (περ. 287 π.Χ- περ. 212 π.Χ.) ήταν Έλληνας μαθηματικός, φυσικός, μηχανικός, εφευρέτης καιαστρονόμος.^[1] Αν και είναι γνωστές λίγες λεπτομέρειες από τη ζωή του, αυτός θεωρείται ως ένας από τους καθοδηγητέςεπιστήμονες στην κλασσική αρχαιότητα. Μεταξύ των προκαταβολών του στη φυσική είναι οι βάσεις τις υδροστατικής στατικής, και μια εξήγηση της αρχής του μοχλού. Αυτός πιστώνεται με τον σχεδιασμό καινοτόμων μηχανών, συμπεριλαμβανομένων τωνπολιορκητικών μηχανών και των αντλιών με κοχλία που φέρουν το όνομά του. Σύγχρονα πειράματα έχουν δοκιμάσει αξιώσεις ότι ο Αρχιμήδης σχεδίασε μηχανές ικανές να επιτίθενται σε πλοία, να τα σηκώνουν έξω από το νερό και να τα πυρπολούν χρησιμοποιώντας μια σειρά από καθρέφτες.^[2]

Ο Αρχιμήδης θεωρείται κατά γενική ομολογία ότι είναι ο σπουδαιότερος από τους μαθηματικούς της αρχαιότητας και ένας από τους σπουδαιότερους όλων των εποχών.^[3][4] Αυτός χρησιμοποίησε τη μέθοδο της εξάντλησης για τον υπολογισμό τηςπεριοχής κάτω από το τόξο παραβολής, με την άθροιση άπειρης σειράς, και έδωσε μια εξαιρετικά ακριβή προσέγγιση για τοναριθμό Πι.^[5] Όρισε επίσης το φαύλο κύκλο που έφερε το όνομά του, φόρμουλες για τον όγκο των επαναστατικών επιφανειώνκαι ένα ευφυές σύστημα για την έκφραση πολύ μεγάλων αριθμών.

Ο Αρχιμήδης πέθανε κατά την πολιορκία των Συρακουσών όταν σκοτώθηκε από ένα Ρωμαίο στρατιώτη, παρά τις εντολές ότι δεν έπρεπε να τον πειράξουν. Ο Κικέρων περιγράφει τον τάφο του Αρχιμήδη που επισκέφτηκε, ο οποίος επιστεφόταν από μιασφαίρα εγγεγραμμένη στο εσωτερικό ενός κυλίνδρου. Ο Αρχιμήδης είχε αποδείξει ότι η σφαίρα είναι τα 2/3 του όγκου της επιφάνειας του κυλίνδρου (συμπεριλαμβανομένων των βάσεων του τελευταίου) και αυτό θεωρείται ως το μεγαλύτερο των μαθηματικών επιτευγμάτων του.

Αντίθετα με τις εφευρέσεις του, τα μαθηματικά κείμενα του Αρχιμήδη ήταν ελάχιστα γνωστά στην αρχαιότητα. Μαθηματικοί από την Αλεξάνδρεια διάβασαν και αναφέρθηκαν σ' αυτόν, η πρώτη κατανοητή ολοκληρωμένη συλλογή δεν ήταν έτοιμη μέχρι περίπου το 530 μ.Χ. από τον Ισίδωρο τον Μιλήσιο, ενώ σχόλια για τα έγγραφά του Αρχιμήδη γράφτηκαν από τον Ευτόσιο και αυτά ανοίχτηκαν (γνωστοποιήθηκαν) στο ευρύτερο κοινό για πρώτη φορά τον έκτο αιώνα μ.Χ.. Τα σχετικά λιγοστά αντίγραφα των γραπτών εργασιών του Αρχιμήδη επιβίωσαν κατά τον Μεσαίωνα όπου ήταν μια πηγή επιρροής ιδεών για τους επιστήμονες κατά τη διάρκεια της Αναγέννησης,^[6] όταν η ανακάλυψη το 1906 από προηγούμενες άγνωστες εργασίες του Αρχιμήδη στο Παλίμψηστο του Αρχιμήδη, παρείχε γνώσεις για το πως κατέληξε σε αυτά τα μαθηματικά του αποτελέσματα.^[7]

Βιογραφία
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Αυτό το μπρούτζινο άγαλμα του Αρχιμήδη είναι στο Παρατηρητήριο Archenhold στο Βερολίνο. Είναι γλυπτό του Gerhard Thieme που παρουσιάστηκε το 1972.

Ο Αρχιμήδης γεννήθηκε περίπου το 287 π.Χ. στην πόλη-λιμάνι των Συρακουσών, στη Σικελία, την εποχή που βρισκόταν ως αποικία κάτω από τη μοναρχική διακυβέρνησή της Μεγάλης Ελλάδας. Η ημερομηνία γέννησής προέρχεται από μια δήλωση του ιστορικού της Ελληνοβυζαντινής Ιωάννη Τζέτζη, και αναφέρει ότι ο Αρχιμήδης έζησε για 75 χρόνια.^[8] Στον Ψαμμίτη, ο Αρχιμήδης δίνει το όνομα του πατέρα του Φειδία, ο οποίος ήταν ένας αστρονόμος, για τον οποίο δεν υπάρχει τίποτα γνωστό. Ο Πλούταρχος έγραψε στο έργο του Βίοι Παράλληλοι ότι ο Αρχιμήδης είχε σχέσεις με τον Βασιλιά Ιέρωνα τον Β΄ τον κυβερνήτη των Συρακουσών.^[9] Μια βιογραφία του Αρχιμήδη είχε γραφτεί από τον φίλο του Ηρακλείδη αλλά η δουλειά του αυτή έχει χαθεί αφήνοντας τις λεπτομέρειες της σκοτεινής του ζωής.^[10] Είναι άγνωστο, για παράδειγμα, αν είχε ποτέ παντρευτεί ή είχε παιδιά. Κατά τη διάρκεια της νεότητας του, ο Αρχιμήδης μπορεί να είχε σπουδάσει στην Αλεξάνδρεια, της Αιγύπτου όπου ο Κόνωνας ο Σάμιος και ο Ερατοσθένης ο Κυρηναίος ήταν σύγχρονοί του. Αυτός αναφέρει τον Κόνωνα τον Σάμιο ως φίλο του, όταν 2 από τα ιστορικά έργα του (Η μέθοδος Μηχανολογικών Θεωρημάτων) και το Πρόβλημα των Βοοειδών έχουν εισαγωγές που απευθύνονται στον Ερατοσθένη.^[a]

Ο Αρχιμήδης πέθανε περίπου το 212 π.Χ. κατά τη διάρκεια του Δευτέρου Καρχηδονιακού Πολέμου, όταν οι ρωμαϊκές δυνάμεις υπό τον στρατηγό Μάρκο Κλαύδιο Μάρκελλο κυρίευσαν την πόλη των Συρακουσών μετά από 2 χρόνων πολιορκία. Σύμφωνα με την λαϊκή παράδοση που μεταφέρθηκε από τον Πλούταρχο ο Αρχιμήδης είχε κατά νου ένα μαθηματικό διάγραμμα όταν η πόλη είχε καταληφθεί. Ένας Ρωμαίος στρατιώτης τον διέταξε να πάει και να γνωρίσει τον στρατηγό Μάρκο Κλαύδιο Μάρκελλο αλλά αυτός αρνήθηκε την πρόταση λέγοντας ότι έπρεπε να τελειώσει με το πρόβλημα του. Ο στρατιώτης εξοργίστηκε και σκότωσε τον Αρχιμήδη με το σπαθί του. Επίσης, ο Πλούταρχος δίνει μια λιγότερο γνωστή άποψη για το θάνατο του Αρχιμήδη που υπονοεί ότι μπορεί να σκοτώθηκε όταν προσπάθησαν να τον παραδώσουν σε έναν Ρωμαίο στρατιώτη. Σύμφωνα με αυτήν την ιστορία, ο Αρχιμήδης κουβαλούσε μαθηματικά όργανά, και τον σκότωσε ο στρατιώτης επειδή νόμιζε ότι ήταν πολύτιμα αντικείμενα. Ο Στρατηγός Μάρκος Κλαύδιος Μάρκελλος όταν πληροφορήθηκε για τον θάνατο του Αρχιμήδη εξοργίστηκε καθώς τον θεωρούσε ως ένα πολύτιμο περιουσιακό στοιχείο της επιστήμης και είχε διατάξει να μην θιγεί.^[11]

Η σφαίρα έχει τα 2/3 του όγκου και της επιφάνειας του κυλίνδρου που την περιβάλλει. Μια σφαίρα και έναςκύλινδρος είχαν τοποθετηθεί στον τάφο του Αρχιμήδη, κατόπιν αιτήσεώς του.

Οι τελευταίες λέξεις που του αποδίδονται είναι «μην ενοχλείτε τους κύκλους μου» (αρχαία: «μή μου τοὺς κύκλους τάραττε»), αναφερόμενος στους κύκλους στο μαθηματικό του σχέδιο το οποίο υποτίθεται ότι μελετούσε όταν τον διέκοψε ο Ρωμαίος στρατιώτης. Συχνά αυτό τιμητικά αποδίδεται στα λατινικά ως «Noli turbare circulos meos», αλλά δεν υπάρχουν αξιόπιστα στοιχεία ότι ο Αρχιμήδης πρόφερε αυτές τις λέξεις και δεν εμφανίζονται στα γραπτά που μας έχουν διασωθεί από τον Πλούταρχο.^[11]

Ο τάφος του Αρχιμήδη είχε ένα γλυπτό που απεικόνιζε την αγαπημένη μαθηματική απόδειξη του, αποτελούμενη από μία σφαίρα και ένα κύλινδρο με το ίδιο ύψος και διάμετρο. Ο Αρχιμήδης είχε αποδείξει ότι ο όγκος και η επιφάνεια της σφαίρας είναι τα δύο τρίτα του κυλίνδρου συμπεριλαμβανομένων των βάσεων. Το 75 π.Χ., 137 χρόνια μετά το θάνατό του, ο Ρωμαίος ρήτορας Κικέρων υπηρετούσε ως κυαίστοραςστη Σικελία. Είχε ακούσει ιστορίες για τον τάφο του Αρχιμήδη, αλλά κανένας από τους ντόπιους δεν ήταν σε θέση να του δώσει τη θέση του τάφου. Ενδεχομένως βρήκε τον τάφο κοντά στην Ακραγαντινή πύλη στις Συρακούσες, σε παραμελημένη κατάσταση και κατάφυτη από θάμνους. Ο Κικέρων διέταξε να καθαρίσουν τον τάφο, και ήταν σε θέση να δει το σκάλισμα και να διαβάσει μερικά από τα εδάφια, που είχαν προστεθεί ως επιγραφή.^[12] Ένα ελληνιστικό μαυσωλείο που ανακαλύφθηκε στην αυλή ενός ξενοδοχείου που ανεγέρθη στις Συρακούσες στις αρχές του 1960, θεωρήθηκε από τον Ciancio ότι είναι εκείνος του Αρχιμήδη, αλλά ο ανασκαφέας, ο έφορος αρχαιοτήτων Συρακουσών, Gentili, προτείνει την ταύτιση με ένα σημαντικό πρόσωπο της εποχής του Αγαθοκλέους (ίσως του ίδιου του βασιλέα).^[13]

Οι βασικές εκδοχές της ζωής του Αρχιμήδη γράφτηκαν πολύ καιρό μετά το θάνατό του από τους ιστορικούς της αρχαίας Ρώμης. Ο απολογισμός της πολιορκίας των Συρακουσών δίνεται από τον Πολύβιο στην Παγκόσμια Ιστορία που γράφτηκε εβδομήντα χρόνια μετά τον θάνατο του Αρχιμήδη, και χρησιμοποιήθηκε στη συνέχεια ως πηγή από τον Πλούταρχο και τον Λίβιο. Αυτό έριξε λίγο φως στον Αρχιμήδη ως πρόσωπο, και επικεντρώθηκε στις πολεμικές μηχανές που λέγεται ότι είχαν κατασκευαστεί για να υπερασπίσουν την πόλη.^[14]

Ανακαλύψεις και εφευρέσεις
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Η Αρχή του Αρχιμήδη

Ο Αρχιμήδης μπορεί να είχε χρησιμοποιήσει την αρχή της πλευστότητας για να καθοριστεί αν η χρυσή κορώνα ήταν λιγότερο πυκνή από το ατόφιο χρυσάφι.

Το πιο γνωστό ανέκδοτο για τον Αρχιμήδη λέει πως εφηύρε μια μέθοδο για τον προσδιορισμό του όγκου ενός αντικειμένου με ακανόνιστο σχήμα.Σύμφωνα με τον Βιτρούβιο, ένα αναθηματικό στέμμα για ένα ναό είχε φτιαχτεί για λογαριασμό του βασιλιά Ιέρωνα Β΄, για το οποίο ο ίδιος είχε προμηθεύσει τον καθαρό χρυσό με τον οποίο θα το έφτιαχναν, και ο Αρχιμήδης κλήθηκε να καθορίσει αν είχε αντικατασταθεί από λίγο ασήμιαπό τον ανέντιμο χρυσοχόο.^[15] Ο Αρχιμήδης έπρεπε να λύσει το πρόβλημα χωρίς να καταστρέψει το στέμμα, έτσι δεν μπορούσε να λιώσει το στέμμα μέσα σε μια κανονικού σχήματος φόρμα προκειμένου να υπολογίσει την πυκνότητα του και την προέλευση του.Καθώς έκανε μπάνιο, παρατήρησε ότι η στάθμη του νερού στην μπανιέρα ανέβηκε όταν μπήκε ο ίδιος μέσα, και συνειδητοποίησε ότι αυτή η επίδραση θα μπορούσε να χρησιμοποιηθεί για τον προσδιορισμό του όγκου του στέμματος. Για πρακτικούς σκοπούς, το νερό είναι ασυμπίεστο,^[16] με αποτέλεσμα το βυθισμένο στέμμα να εκτοπίσει μια ποσότητα νερού ίση με τον δικό του όγκο. Διαιρώντας την μάζα του στέμματος με τον όγκο του νερού που εκτοπίζεται, προκύπτει η πυκνότητα του στέμματος. Αυτή η πυκνότητα θα είναι μικρότερη από εκείνη του χρυσού, εάν κάποια φθηνότερα και λιγότερο πυκνά μέταλλα είχαν προστεθεί. Ο Αρχιμήδης στη συνέχεια βγήκε στους δρόμους γυμνός, τόσο ενθουσιασμένος από την ανακάλυψή του που ξέχασε να ντυθεί, φωνάζοντας και κλαίγοντας : "Εύρηκα! Εύρηκα!". Το πείραμά του διεξήχθη με επιτυχία αποδεικνύοντας ότι είχε νοθευτεί με σίδερο.^[17]

Η ιστορία του χρυσού στέμματος δεν εμφανίζεται στα γνωστά έργα του Αρχιμήδη. Επιπλέον, η πρακτικότητα της μεθόδου που περιγράφει έχει αμφισβητηθεί, λόγω της ακραίας ακρίβειας που χρειάζεται κάποιος για να μετρήσει τη μετατόπιση νερού.^[18] Αντ' αυτού ο Αρχιμήδης αναζήτησε μια λύση της υδροστατικής που αναφέρεται ως η γνωστή αρχή του Αρχιμήδη, την οποία ο ίδιος περιγράφει στο σύγγραμμά του Περί επιπλέοντων σωμάτων. Αυτή η αρχή δηλώνει ότι ένα σώμα που βυθίζεται σε ένα ρευστό δέχεται μια δύναμη άνωσης ίση με το βάρος του υγρού που εκτοπίζει.^[19] Χρησιμοποιώντας αυτή την αρχή, θα ήταν δυνατή η σύγκριση της πυκνότητας της χρυσής στεφάνης με εκείνη του στερεού χρυσού με την εξισορρόπηση της κορώνας σε ένα ζυγό με ένα δείγμα αναφοράς χρυσού, και στη συνέχεια βυθίζοντας τη συσκευή στο νερό. Η διαφορά πυκνότητας μεταξύ των δύο δειγμάτων θα μπορούσε να προκαλέσει την κλίμακα να ανατραπεί αναλόγως.Ο Γαλιλαίος έκρινε ότι «πιθανολογείται ότι η μέθοδος αυτή είναι η ίδια που ακολούθησε ο Αρχιμήδης, δεδομένου ότι, εκτός του ότι είναι πολύ ακριβής, βασίζεται σε επιδείξεις που παρουσιάσε ο Αρχιμήδης ο ίδιος".^[20] Σε ένα κείμενο του 12ου αιώνα με τίτλο Mappae clavicula υπάρχουν οδηγίες για το πώς να εκτελέσει κανείς τις ζυγίσεις στο νερό προκειμένου να υπολογίσει το ποσοστό του αργύρου που χρησιμοποιήθηκε, και ως εκ τούτου την επίλυση του προβλήματος.^[21][22] Το λατινικό ποίημα Carmen de ponderibus et mensuris του 4ου ή 5ου αιώνα περιγράφει τη χρήση της υδραυλικής ισορροπίας για την επίλυση του προβλήματος της κορώνας, και αποδίδει την μέθοδο στον Αρχιμήδη.^[21]

Κοχλίας του Αρχιμήδη
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Κύριο λήμμα: Κοχλίας του Αρχιμήδη

Ο κοχλίας του Αρχιμήδη μπορεί να ανεβάσει το νερό αποτελεσματικά.

Ένα μεγάλο μέρος του έργου του Αρχιμήδη στη μηχανική προέκυψε από την εκπλήρωση των αναγκών της γεννέτηρας πόλης του των Συρακουσών. Ο Έλληνας Αθηναίος συγγραφέας Ναύκρατις περιέγραψε πώς ο βασιλιάς Ιέρων Β΄ανέθεσε στον Αρχιμήδη να σχεδιάσει ένα τεράστιο πλοίο, τη Συρακουσία, το οποία θα μπορούσε να χρησιμοποιηθεί για ταξίδια πολυτελείας, για μεταφορά προμηθειών και ως ναυτικό πολεμικό πλοίο.^[23] Σύμφωνα με τον Αθήναιο, ήταν ικανό να μεταφέρει 600 άτομα και περιλάμβανε διακοσμητικούς κήπους, ένα γυμναστήριοκαι ένα ναό αφιερωμένο στη θεά Αφροδίτη μεταξύ των εγκαταστάσεών του. Δεδομένου ότι σε ένα πλοίο αυτού του μεγέθους θα διέρρεε ένα σημαντικό ποσό νερού διαμέσου του κύτους, ο κοχλίας του Αρχιμήδη υποτίθεται ότι αναπτύχθηκε με σκοπό την απομάκρυνση του νερού. Η μηχανή του Αρχιμήδη ήταν μια συσκευή με ένα περιστρεφόμενο κοχλία σε σχήμα λεπίδας μέσα σε έναν κύλινδρο. Γυρνούσε χειροκίνητα και μπορούσε επίσης να χρησιμοποιηθεί για τη μεταφορά νερού από ένα χαμηλού επίπεδου σώμα του νερού σε κανάλια άρδευσης. Ο κοχλίας του Αρχιμήδη είναι ακόμα σε χρήση σήμερα για την άντληση υγρών και στερεών σε κόκκους, όπως ο άνθρακας και το σιτάρι. Ο κοχλίας του Αρχιμήδη όπως περιγράφονταν στα ρωμαϊκά χρόνια από τον Βιτρούβιο μπορεί να ήταν μια βελτίωση σε σχέση με μία αντλία-κοχλία που είχε χρησιμοποιηθεί για την άρδευση των Κρεμαστών Κήπων της Βαβυλώνας.^[24][25][26]Το πρώτο στον κόσμο θαλασσοπόρο ατμόπλοιο με βιδωτή έλικα ήταν το SS Archimedes, το οποία ξεκίνησε να λειτουργεί το 1839 και ονομάστηκε έτσι προς τιμήν του Αρχιμήδη και του έργου του πάνω στον κοχλία.^[27]

Αρπάγη του Αρχιμήδη
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Η Αρπάγη του Αρχιμήδη είναι ένα όπλο που λέγεται ότι είχε σχεδιαστεί με σκοπό να υπερασπιζόταν την πόλη των Συρακουσών. Επίσης γνωστή ως "αναδευτής πλοίων", η αρπάγη αποτελούνταν από ένα βραχίονα-γερανό, από τον οποίο αναπτύσσονταν ένας μεγάλος μεταλλικός γάντζος. Όταν η αρπάγη θα έπεφτε πάνω στο επιτιθέμενο πλοίο ο βραχίονας θα ταλαντευόταν προς τα πάνω, σηκώνοντας το πλοίο έξω από το νερό με την πιθανότητα να το ναυαγήσει. Υπήρξαν σύγχρονα πειράματα για να ελεγχθεί η σκοπιμότητα της Αρπάγης και το 2005 ένα τηλεοπτικό ντοκιμαντέρ με τίτλο Υπερόπλα του Αρχαίου Κόσμου, κατασκεύασε μια έκδοση της Αρπάγης και κατέληξε στο συμπέρασμα ότι ήταν μια λειτουργική συσκευή.^[28][29]

Άγαλμα του Αρχιμήδη σε ένα πάρκο του Βερολίνου.

Έλιξ του Αρχιμήδους

Ακτίνα φωτός
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Ο Αρχιμήδης μπορεί να χρησιμοποίησε καθρέπτες οι οποίοι λειτουργούσαν συγκεντρωτικά σανπαραβολικό κάτοπτρο και έκαιγαν τα πλοία που επιτίθονταν στις Συρακούσες.

Το 2ο αιώνα μ.Χ. ο συγγραφέας Λουκιανός έγραψε ότι κατά τη διάρκεια της Πολιορκίας των Συρακουσών (214-212 π.Χ.), ο Αρχιμήδης κατέστρεψε εχθρικά πλοία με τη χρήση της φωτιάς. Αιώνες αργότερα, ο Ανθέμιος ο Τραλλιανός αναφέρει τοφλεγόμενο γυαλί ως το όπλο του Αρχιμήδη.^[30]. Η συσκευή, γνωστή και ως "Ακτίνα φωτός του Αρχιμήδη", χρησιμοποιούνταν για να συγκεντρώνει το ηλιακό φως στα επερχόμενα πλοία, με αποτέλεσμα αυτά να παίρνουν φωτιά.

Αυτό το υποτιθέμενο όπλο υπήρξε θέμα συνεχόμενης διαμάχης από την Αναγέννηση. Ο Ρενέ Ντεκάρτ το απέρριψε ως λανθασμένο, ενώ νέες έρευνες έχουν αποπειραθεί να αναπαραστήσουν το αποτέλεσμα χρησιμοποιώντας μόνο τα μέσα που ήταν διαθέσιμα στον Αρχιμήδη.^[31] Έχει προταθεί ότι μια μεγάλη παράταξη από αρκετά γυαλισμένες μπρούτζινες ή χάλκινεςασπίδες οι οποίες λειτουργούσαν σαν καθρέπτες θα μπορούσαν να είχαν χρησιμοποιηθεί για να συγκεντρώσουν το ηλιακό φως στο πλοίο. Αυτό θα βασιζόταν στην αρχή του παραβολικού κατόπτρου με παρόμοιο τρόπο όπως σε έναν ηλιακό φούρνο.

Ένα τεστ της ακτίνας φωτός του Αρχιμήδη έγινε το 1973 από τον Έλληνα επιστήμονα Ιωάννη Σάκκα. Το πείραμα έλαβε χώρα στη ναυτική βάση του Σκαραμαγκά έξω από την Αθήνα. Για αυτή τη περίπτωση χρησιμοποιήθηκαν 70 καθρέπτες, ο καθένας με χάλκινη επίστρωση και μέγεθος περίπου στα 1,5 επί 1m. Οι καθρέπτες στράφηκαν σε ένα ομοίωμα από κόντρα πλακέ ενός Ρωμαϊκού πολεμικού πλοίου το οποίο βρισκόταν σε απόσταση κοντά στα 50m. Όταν οι καθρέπτες σημάδεψαν με ακρίβεια το πλοίο, αυτό έπιασε φωτιά μέσα σε λίγα δευτερόλεπτα. Το πλοίο από κόντρα πλακέ ήταν επιστρωμένο με βαφή πίσσας, η οποία μπορεί να βοήθησε στην ανάφλεξη.^[32] Η επίστρωση με βαφή πίσσας ήταν κοινότοπη στα πλοία την κλασσική εποχή.^[d]

Τον Οκτώβριο του 2005 μια ομάδα φοιτητών του Τεχνολογικού Ινστιτούτου Μασαχουσέτης διεξήγαγε ένα πείραμα με 127 τετραγωνικά κεραμίδια καθρέπτη 30cm, στοχεύοντας ένα ομοίωμα ξύλινου πλοίου σε απόσταση περίπου 30m. Φλόγες ξέσπασαν σε ένα μπάλωμα του πλοίου αλλά μόνο όταν ο ουρανός δεν είχε σύννεφα και το πλοίο παρέμεινε στη θέση του για περίπου 10 λεπτά. Προέκυψε το συμπέρασμα ότι η παράταξη ήταν ένα εφικτό όπλο κάτω από αυτές τις συνθήκες. Η ομάδα του ΜΙΤ επανέλαβε το πείραμα για την τηλεοπτική εκπομπή MythBusters, χρησιμοποιώντας μια ξύλινη βάρκα ψαρέματος στο Σαν Φρανσίσκο ως στόχο. Ξανά συνέβη μερική απανθράκωση, μαζί με μια μικρή φωτιά. Για να πιάσει φωτιά, το ξύλο χρειάζεται να φτάσει στη θερμοκρασία αυτανάφλεξης, που είναι γύρω στους 300 °C.^[33][34]

Όταν οι Mythbusters πρόβαλλαν το αποτέλεσμα του πειράματος στο Σαν Φρανσίσκο τον Ιανουάριο του 2006 ο μύθος τοποθετήθηκε στην κατηγορία των «αποτυχημένων» λόγω του χρόνου και των ιδανικών καιρικών συνθηκών που χρειαζόταν για να συμβεί η ανάφλεξη. Επίσης τονίστηκε ότι αφού οι Συρακούσες έβλεπαν την θάλασσα προς τα ανατολικά, ο ρωμαϊκός στόλος θα έπρεπε να επιτεθεί κατά τη διάρκεια του πρωινού για βέλτιστη συγκέντρωση φωτός από τους καθρέπτες. Οι Mythbusters τόνισαν επίσης ότι συμβατικά όπλα όπως φλεγόμενα βέλη ή βίδες από τους καταπέλτες θα ήταν ένας πολύ εύκολος τρόπος για να βάλουν φωτιά σε ένα πλοίο σε κοντινές αποστάσεις.^[2]

Τον Δεκέμβριο του 2010, οι Mythbusters άνοιξαν ξανά την υπόθεση της ακτίνας φωτός σε ένα σπέσιαλ επεισόδιο όπου συμμετείχε και οΜπαράκ Ομπάμα με τον τίτλο "Η Πρόκληση του Προέδρου". Αρκετά πειράματα διεξήχθησαν, συμπεριλαμβανομένης και μιας δοκιμής μεγάλης κλίμακας με 500 μαθητές να σημαδεύουν με τους καθρέπτες ένα ομοίωμα ενός Ρωμαϊκού πλοίου σε απόσταση 120m. Σε όλα τα πειράματα το ιστίο απέτυχε να φτάσει στους 210 °C που απαιτούνται για να πιάσει φωτιά και ο μύθος τοποθετήθηκε εκ νέου στην κατηγορία των «αποτυχημένων». Η εκπομπή συμπέρανε πως ένα πιο πιθανό αποτέλεσμα των καθρεφτών θα ήταν να τυφλώνει, να εκθαμβώνει και να αποσπά την προσοχή του πληρώματος του πλοίου. ^[35]

Άλλες ανακαλύψεις και εφευρέσεις
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Παρότι δεν ήταν ο Αρχιμήδης που εφηύρε τον μοχλό, έδωσε μια εξήγηση για την αρχή στην οποία βασίζεται η χρήση του στο έργο του Περί επιπέδων ισορροπιών. Αρχαιότερες περιγραφές του μοχλού μπορούν να βρεθούν στην Περιπατητική Σχολή των υποστηρικτών του Αριστοτέλη και μερικές φορές αυτές αποδίδονται στον Αρχύτα.^[36][37] Σύμφωνα με τον Πάππο τον Αλεξανδρέα, το έργο του Αρχιμήδη πάνω στους μοχλούς τον έκανε να παρατηρήσει: «Δώστε μου ένα σημείο να στηριχθώ και θα κινήσω τη Γη» (αρχαία: δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω).^[38] O Πλούταρχος περιγράφει πώς ο Αρχιμήδης σχεδίαζε ανυψωτικά συστήματα τροχαλιών επιτρέποντας στους ναυτικούς να χρησιμοποιούν την αρχή της μόχλευσης για να σηκώνουν αντικείμενα που ειδάλλως δεν θα μπορούσαν να σηκώσουν.^[39] Στον Αρχιμήδη επίσης αποδίδεται η βελτίωση της δύναμης και της ακρίβειας του καταπέλτη καθώς και η εφεύρεση του οδομετρητή κατά τη διάρκεια του πρώτου Καρχηδονιακού πολέμου. Ο οδομετρητής περιγράφεται ως ένα κάρο με μηχανισμό γραναζιού που έριχνε μια μπάλα σε ένα κιβώτιο κάθε φορά που συμπλήρωνε ένα μίλι.^[40] Επίσης κατασκεύασε ένα υδραυλικό ρολόι το οποίο υπολόγιζε με μεγάλη ακρίβεια τις ώρες και ειδοποιούσε για την αλλαγή της ώρας.

Ο Κικέρων(106-43π.Χ.) αναφέρει εν συντομία τον Αρχιμήδη στο διάλογό του Περί δημοκρατίας, που απεικονίζει μια φανταστική συζήτηση η οποία λαμβάνει χώρα το 129π.Χ.. Μετά την κατάκτηση των Συρακουσών το 212 π.Χ. λέγεται ότι ο Στρατηγός Μάρκος Κλαύδιος Μάρκελλος πήρε πίσω στη Ρώμη δύο μηχανισμούς, που κατασκευάσθηκαν από τον Αρχιμήδη και με εφαρμογή στην αστρονομία, το οποίο έδειχνε την κίνηση του Ηλίου, της Σελήνης και πέντε πλανητών. Ο Κικέρων αναφέρει παρόμοιους μηχανισμούς σχεδιασμένους από τον Θαλή τον Μιλήσιο και τον Εύδοξο τον Κνίδιο. Ο διάλογος λέει πως ο Μάρκελλος κράτησε τον ένα από τους μηχανισμούς ως το μοναδικό προσωπικό λάφυρο από τις Συρακούσες και δώρισε τον άλλο στο Ναό της Αρετής στη Ρώμη. Ο μηχανισμός του Μάρκελλου παρουσιάστηκε από τον Γάιο Σουλπίκιο Γάλλο στον Λούκιο Φούριο Φίλο ο οποίος τον περιέγραψε:

Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione. —Όταν ο Γάλλος μετακίνησε την υδρόγειο, τότε η Σελήνη ακολούθησε τον Ήλιο σε όσες στροφές και αν έκανε σε αυτή τη μπρούντζινη συσκευή όπως θα γινόταν και στον ουρανό, από την οποία είδαμε ότι επίσης στον ουρανό η έκλειψη Ηλίου ήταν η ίδια όταν η Σελήνη ερχόταν σε εκείνη την θέση ώστε να ρίχνει την σκιά της πάνω στην Γη, όταν τα τρία σώματα ήταν ευθυγραμμισμένα.^[41][42]

Αυτή είναι η περιγραφή ενός πλανητάριου ή πλανητοσκοπίου. Ο Πάππος ο Αλεξανδρεύς δήλωσε ότι ο Αρχιμήδης είχε γράψει ένα χειρόγραφο (σήμερα χαμένο) πάνω στην κατασκευή τέτοιων μηχανισμών με το τίτλο Περί σφαιροποιΐας. Πρόσφατες έρευνες σε αυτό το θέμα εστιάζουν στον Μηχανισμό των Αντικυθήρων, άλλη μία συσκευή από την κλασσική αρχαιότητα που πιθανότατα σχεδιάστηκε για τον ίδιο λόγο. Η δημιουργία τέτοιου είδους μηχανισμών θα απαιτούσε προχωρημένη γνώση για τη λειτουργία τουδιαφορικού. Αυτό πιστευόταν ότι ήταν πέρα των δυνατοτήτων της τεχνολογίας στις αρχαίες εποχές, αλλά η ανακάλυψη του Μηχανισμού των Αντικυθήρων το 1902 επιβεβαίωσε το γεγονός ότι συσκευές τέτοιου είδους ήταν γνωστές στους αρχαίους Έλληνες.^[43][44]

Μαθηματικά
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Ενώ συχνά θεωρείται ως σχεδιαστής μηχανικών συσκευών, ο Αρχιμήδης έκανε επίσης συνεισφορές στον τομέα των Μαθηματικών. Ο Πλούταρχος έγραψε: "Αφιέρωσε όλη του τη στοργή και τη φιλοδοξία του σε αυτές τις καθαρότερες εικασίες όπου δεν μπορεί να γίνει αναφορά στις χυδαίες ανάγκες της ζωής."^[45]

Ο Αρχιμήδης χρησιμοποίησε τοΠυθαγόρειο θεώρημα για να υπολογίσει την πλευρά του 12-γωνου από αυτή τουεξαγώνου και για κάθε επακόλουθο διπλασιασμό των πλευρών του κανονικού πολυγώνου.

Ο Αρχιμήδης μπορούσε να χρησιμοποιήσει τα απειροελάχιστα με τρόπο παρόμοιο με τον Ολοκληρωτικό Λογισμό. Μέσω της Εις άτοπον απαγωγή απόδειξη μπορούσε να δώσει απαντήσεις σε προβλήματα έως ένα αυθαίρετο βαθμό ακρίβειας, προσδιορίζοντας τα όρια μέσα στα οποία ίσχυε η απάντηση. Αυτή η μέθοδος είναι γνωστή ως η Μέθοδος της εξάντλησης και την εφάρμοσε για να προσεγγίσει την τιμή του αριθμού π. Στο Κύκλου Μέτρησις το έκανε αυτό ζωγραφίζοντας ένα μεγαλύτερο κανονικό εξάγωνο έξω από τον κύκλο και ένα μικρότερο κανονικό εξάγωνο μέσα στο κύκλο και προοδευτικά διπλασιάζοντας τον αριθμό των πλευρών και στα δύο κανονικά πολύγωνα, υπολογίζοντας το μήκος της πλευράς κάθε πολυγώνου σε κάθε βήμα. Καθώς ο αριθμός των πλευρών αυξάνεται, γίνεται μια πιο ακριβής προσέγγιση του κύκλου. Μετά από 4 τέτοια βήματα, όταν τα πολύγωνα είχαν από 96 πλευρές το καθένα, ήταν σε θέση να προσδιορίσει ότι η τιμή του π βρισκόταν ανάμεσα στο 3¹⁄₇(περίπου 3.1429) και 3¹⁰⁄₇₁(περίπου 3.1408) εντός των ορίων αφού η τιμή προσεγγιστικά είναι 3.1416.^[46] Επίσης απέδειξε ότι το Εμβαδόν ενός κύκλου ισούται με το π πολλαπλασιασμένο με το τετράγωνο της ακτίνας του κύκλου (πr²). Στο Περί σφαίρας και κυλίνδρου δηλώνει ότι ένα μέγεθος όταν προστεθεί αρκετές φορές στον εαυτό του θα ξεπεράσει οποιοδήποτε άλλο μέγεθος. Αυτή είναι η Αρχιμήδεια Ιδιότητα των πραγματικών αριθμών.^[47]

Στο Κύκλου Μέτρησις ο Αρχιμήδης υποστηρίζει ότι η τετραγωνική ρίζα του 3 βρίσκεται ανάμεσα στο ²⁶⁵⁄₁₅₃ (περίπου 1.7320261) και στο¹³⁵¹⁄₇₈₀ (περίπου 1.7320512). Η πραγματική τιμή είναι περίπου 1.7320508, γεγονός που κάνει αυτό τον υπολογισμό πολύ ακριβή. Παρουσίασε αυτό το αποτέλεσμα χωρίς να προσφέρει καμία εξήγηση για το πως έφτασε σε αυτό. Αυτή η όψη του έργου του Αρχιμήδη ανάγκασε τον John Wallis να δηλώσει: "πιθανόν να κάλυψε τα ίχνη της ερευνάς του σκόπιμα επειδή θα ένιωθε ότι δίνει στους μεταγενέστερους το μυστικό της συλλογής πληροφοριών του, ενώ ταυτόχρονα ήθελε να αποσπάσει από αυτούς απαντήσεις για τα δικά του ευρήματα".^[48] Είναι πιθανό να χρησιμοποιούσε επαναληπτικές διαδικασίες για να υπολογίσει αυτές τις τιμές.^[49]

Όπως αποδείχθηκε από τον Αρχιμήδη το εμβαδόν του παραβολικούτμήματος στην πάνω εικόνα είναι ίσο με τα 4/3 του εμβαδού του εγγεγραμένου τριγώνου στην κάτω εικόνα.

Στο Τετραγωνισμός της παραβολής ο Αρχιμήδης απέδειξε ότι το εμβαδόν που περικλείεται από μία παραβολή και μια ευθεία γραμμή είναι⁴⁄₃ φορές το εμβαδόν του αντίστοιχου εγγεγραμμένου τριγώνου όπως φαίνεται στην εικόνα δεξιά. Εξέφρασε τη λύση στο πρόβλημα ως μίαάπειρη Γεωμετρική σειρά με λόγο ¹⁄₄.

Αν ο πρώτος όρος σε αυτή τη σειρά είναι το εμβαδόν του τριγώνου, τότε ο δεύτερος είναι το άθροισμα των εμβαδών των δύο τριγώνων των οποίων οι βάσεις είναι οι δύο μικρότερες διατέμνουσες γραμμές και ούτω καθεξής. Αυτή η απόδειξη χρησιμοποιεί μια παραλλαγή της σειράς 1/4 + 1/16 + 1/64 + 1/256 +... η οποία έχει άθροισμα το ¹⁄₃.

Στο Ψαμμίτης, ξεκινά να υπολογίζει τον αριθμό των κόκκων άμμου που υπάρχουν στο σύμπαν. Στη προσπάθεια του, αντιτάχθηκε στην ιδέα ότι ο αριθμός των κόκκων άμμου ήταν πολύ μεγάλος για να υπολογισθεί. Έγραψε: "Υπάρχουν μερικοί, βασιλιά Γέλωνα (Γέλων ο Β', γιος του Ιέρωνα Β') που πιστεύουν ότι ο αριθμός της άμμου είναι άπειρος σε μέγεθος και όταν λέω άμμου δεν εννοώ την άμμο που υπάρχει στις Συρακούσες και στην υπόλοιπη Σικελία αλλά και αυτή που βρίσκεται σε κάθε περιοχή είτε κατοικείται είτε όχι". Για να λύσει το πρόβλημα, ο Αρχιμήδης επινόησε ένα σύστημα μέτρησης με μονάδα μέτρησης την μυριάδα. Η λέξη προέρχεται από τη λέξη μυριάς, για τον αριθμό 10.000. Πρότεινε ένα σύστημα αρίθμησης χρησιμοποιώντας μυριάδα μυριάδων (100 εκατομμύρια) και συμπέρανε ότι ο αριθμός των κόκκων άμμου που χωράει το σύμπαν είναι 8 εικοσάκις εκατομμύρια ή 8 × 10⁶³ .^[50]

Συγγράμματα
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Τα έργα του Αρχιμήδη είχαν γραφτεί στη δωρική διάλεκτο, τη διάλεκτο των αρχαίων Συρακουσών.^[51] Τα γραπτά έργα του δεν έχουν διασωθεί όπως αυτά του Ευκλείδη, κι επτά από τις πραγματείες του είναι γνωστό ότι υπήρχαν μόνο μέσα από αναφορές που γίνονται σε αυτές από άλλους συγγραφείς. Ο Πάππος ο Αλεξανδρεύς αναφέρει το έργο του Αρχιμήδη Περί σφαιροποιΐας καθώς κι ένα άλλο πάνω σταπολύεδρα, ενώ ο Θέων ο Αλεξανδρεύς κάνει μία παρατήρηση σχετικά με τη διάθλαση από το μη διασωθέν σήμερα έργο του ΑρχιμήδηΚάτοπτρα.^[b] Κατά τη διάρκεια της ζωής του, ο Αρχιμήδης έκανε το έργο του γνωστό μέσω αλληλογραφίας με τους μαθηματικούς στην Αλεξάνδρεια. Τα γραπτά του Αρχιμήδη συλλέχθηκαν από έναν αρχιτέκτονα της Βυζαντινής Αυτοκρατορίας ονόματι Ισίδωρος ο Μιλήσιος (περ. 530 μ.Χ.), ενώ τα σχόλια για τα έργα του Αρχιμήδη γραμμένα από τονΕυτόχιο στον έκτο μ.Χ. αιώνα, βοήθησαν να διαδοθεί το έργο του σε ένα ευρύτερο κοινό. Έργο του Αρχιμήδη μεταφράστηκε στα αραβικά από τον Ταμπίτ ιμπν Κουρά (836-901 μ.Χ.), και στη λατινική^[52] από τον Γεράρδο της Κρεμόνα (περ. 1114-1187 μ.Χ.). Κατά τη διάρκεια της Αναγέννησης, η Editio Princeps (Πρώτη έκδοση), δημοσιεύθηκε στη Βασιλείατο 1544 από τον Johann Herwagen, με τα έργα του Αρχιμήδη στην ελληνική και λατινική. Περί το έτος 1586, ο Γαλιλαίος Γαλιλέι εφηύρε ένα υδροστατικό ζυγό για τη ζύγιση των μετάλλων στον αέρα και στο νερό, εμπνευσμένος προφανώς από το έργο του Αρχιμήδη.^[53]

Διασωθέντα συγγράμματα
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Ο Αρχιμήδης λέγεται πως διατύπωσε την εξής πρόταση σχετικά με το μοχλό:"Δώστε μου ένα μέρος για να σταθώ και θα μετακινήσω ακόμα κι ολόκληρη τη Γη."

• Περί επιπέδων ισορροπιών ή κέντρα βαρών επιπέδων ή Μηχανικά, Βιβλ α' και β'

Το πρώτο βιβλίο αποτελείται από δεκαπέντε προτάσεις και επτά αξιώματα, ενώ το δεύτερο βιβλίο περιέχει δέκα προτάσεις. Σε αυτό το έργο του ο Αρχιμήδης εξηγεί το Νόμο του Μοχλού δηλώνοντας ότι:

"Τα μεγέθη είναι σε ισορροπία, όταν βρίσκονται σε αποστάσεις αντιστρόφως ανάλογες με το βάρος τους."

Ο Αρχιμήδης χρησιμοποιεί τις αρχές που προκύπτουν, για τον υπολογισμό των εμβαδών και των κέντρων βάρους των διαφόρων γεωμετρικών σχημάτων, όπως τρίγωνα, παραλληλόγραμμα και παραβολές.^[54]

• Κύκλου μέτρησις. Σώζονται τρία θεωρήματα.

Αυτή είναι μια σύντομη εργασία που αποτελείται από τρεις προτάσεις. Είναι γραμμένη σε μορφή αλληλογραφίας με τον Δοσίθεο του Πηλουσίου, ο οποίος ήταν μαθητής του Κόνωνα του Σάμιου. Στη δεύτερη πρόταση, ο Αρχιμήδης δίνει μια προσέγγιση της αξίας του π, η οποία δείχνει ότι είναι μεγαλύτερη από ²²³⁄₇₁ και μικρότερη από ²²⁄₇.

• Περί ελίκων (28 προτάσεις, 6 πορίσματα)

Αυτό το έργο των 28 προτάσεων, επίσης απευθυνόταν στον Δοσίθεο. Τούτη η πραγματεία ορίζει αυτό που σήμερα καλείται η σπείρα του Αρχιμήδη. Είναι ο γεωμετρικός τόπος των σημείων που αντιστοιχούν στο σύνολο των διάφορων θέσεων, από τις οποίες περνάει ένα σημείο, με την πάροδο του χρόνου, καθώς αυτό κινείται μακριά από ένα σταθερό σημείο με μια σταθερή ταχύτητα κατά μήκος μίας γραμμής, η οποία περιστρέφεται με σταθερή γωνιακή ταχύτητα. Ισοδύναμα, σεπολικές συντεταγμένες (r, θ) μπορεί να περιγραφεί από την εξίσωση

με πραγματικούς αριθμούς a και b. Αυτό είναι ένα πρώιμο παράδειγμα μιας μηχανικής καμπύλης (καμπύλη που διαγράφεται από ένα κινούμενο σημείο), που θεωρείται από Έλληνα μαθηματικό.

• Περί σφαίρας και κυλίνδρου, Βιβλίο α' και β'

Στην πραγματεία αυτή απευθυνόμενος στον Δοσίθεο, ο Αρχιμήδης κατορθώνει κάτι το οποίο τον έκανε να είναι ιδιαίτερα περήφανος. Αυτό το κάτι ήταν η ανακάλυψη της σχέσης μεταξύ μίας σφαίρας κι ενός περιγεγραμμένου κυλίνδρου του ίδιου ύψους και της ίδιας διαμέτρου. Ο όγκος είναι ⁴⁄₃πr³ για τη σφαίρα, και 2πr³ για τον κύλινδρο. Το εμβαδόν επιφανείας είναι 4πr² για τη σφαίρα, και 6πr² για τον κύλινδρο (συμπεριλαμβανομένων των δύο βάσεων του), όπου r είναι η ακτίνα της σφαίρας και του κυλίνδρου. Η σφαίρα έχει όγκο τα δύο τρίτα του περιγεγραμμένου κυλίνδρου. Ομοίως, η σφαίρα έχει εμβαδόν τα δύο τρίτα του κυλίνδρου (συμπεριλαμβανομένων των βάσεων). Αξίζει να σημειωθεί πως στον τάφο του Αρχιμήδη, κατόπιν αιτήσεώς του είχαν τοποθετηθεί δύο γλυπτά, μία σφαίρα κι ένας κύλινδρος.

• Περί κωνοειδέων και σφαιροειδέων (32 προτάσεις, 1 πόρισμα)

Αυτό είναι ένα έργο αποτελούμενο από 32 προτάσεις, που απευθύνονται στον Δοσίθεο. Σε αυτή την πραγματεία του ο Αρχιμήδης υπολογίζει τα εμβαδά και τους όγκουςτμημάτων από κώνους, σφαίρες και παραβολοειδή.

• Πρόβλημα Βοεικόν

Το έργο ανακαλύφθηκε από τον Gotthold Ephraim Lessing σε ένα ελληνικό χειρόγραφο αποτελούμενο από ένα ποίημα από 44 γραμμές, στη βιβλιοθήκη Herzog August στοWolfenbüttel της Γερμανίας, το 1773. Απευθύνεται στον Ερατοσθένη και στους μαθηματικούς στην Αλεξάνδρεια. Ο Αρχιμήδης τους προκαλεί να μετρήσουν τον αριθμό των βοοειδών στην Αγέλη του Ήλιου, με την ταυτόχρονη επίλυση ενός αριθμού Διοφαντικών εξισώσεων. Υπάρχει και μια πιο δύσκολη έκδοση του προβλήματος στην οποία μερικές από τις λύσεις απαιτείται να είναι τέλεια τετράγωνα. Αυτή η έκδοση του προβλήματος λύθηκε για πρώτη φορά από τον Α. Amthor^[55] το 1880 και η απάντηση είναι ένας πολύ μεγάλος αριθμός, περίπου 7,760271 × 10^206544.[56]

• Ψαμμίτης

Σε αυτή την πραγματεία του, ο Αρχιμήδης μετρά τον αριθμό των κόκκων της άμμου που μπορούν να χωρέσουν μέσα στο σύμπαν. Το βιβλίο αναφέρει την ηλιοκεντρική θεωρία του ηλιακού συστήματος που προτείνεται από τον Αρίσταρχο το Σάμιο, καθώς και σύγχρονες ιδέες σχετικά με το μέγεθος της Γης και την απόσταση μεταξύ διάφορων ουράνιων σωμάτων. Με τη χρήση ενός συστήματος αριθμών υψωμένων σε μυριάδες(μυριάδα=10.000), ο Αρχιμήδης καταλήγει πως ο αριθμός των κόκκων της άμμου που απαιτείται για να γεμίσει το σύμπαν είναι 8 x 10⁶³ σε σύγχρονη σημειογραφία. Η εισαγωγική επιστολή αναφέρει ότι ο πατέρας του Αρχιμήδη ήταν αστρονόμος ονόματι Φειδίας. Ο Ψαμμίτης είναι το μόνο σωζόμενο έργο στο οποίο ο Αρχιμήδης συζητά τις απόψεις του σχετικά με την αστρονομία.^[57]

• Τετραγωνισμός παραβολής

Στο έργο αυτό που αποτελείται από 24 προτάσεις ο Αρχιμήδης απευθυνόμενος στο Δοσίθεο, αποδεικνύει με δύο μεθόδους ότι το εμβαδόν που περικλείεται από μιαπαραβολή και μια ευθεία γραμμή ισούται με ⁴⁄₃ πολλαπλασιαζόμενο επί το εμβαδό ενός τριγώνου με την ίδια βάση και ύψος. Αυτό το κατάφερε με τον υπολογισμό της αξίας τηςγεωμετρικής σειράς που αθροίζεται στο άπειρο με λόγο ¹⁄₄.

Πρόσφατα (2006) διαβάστηκαν από το Παλίμψηστο του Αρχιμήδη αποσπάσματα από τα έργα που διασώθηκαν σε αυτό:

• Οστομάχιον
  Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Αυτό είναι ένα τεμαχισμένο παζλ παρόμοιο με ένα tangram, κι η πραγματεία που το περιέγραφε βρέθηκε σε πιο ολοκληρωμένη μορφή στο Παλίμψηστο του Αρχιμήδη. Ο Αρχιμήδης υπολογίζει τα εμβαδά των δεκατεσσάρων κομματιών, τα οποία συναρμολογούμενα μπορούν να σχηματίσουν ένα τετράγωνο. Έρευνα που δημοσιεύθηκε το 2003 από τον Δρ.Reviel Netz του Πανεπιστημίου του Στάνφορντ, υποστήριζε ότι ο Αρχιμήδης προσπαθούσε να καθορίσει με πόσους δυνατούς τρόπους θα μπορούσαν να τοποθετηθούν τα κομμάτια έτσι ώστε να συναρμολογήσουν ένα τετράγωνο. Ο Δρ Netz υπολογίζει πως τα κομμάτια μπορούν να δημιουργήσουν ένα τετράγωνο με 17.152 διαφορετικούς τρόπους.^[58] Ο αριθμός των διατάξεων είναι 536, όταν οι λύσεις που είναι ισοδύναμες με περιστροφή κι αντανάκλαση έχουν αποκλειστεί.^[59] Το παζλ αντιπροσωπεύει ένα παράδειγμα πρώιμου προβλήματος στη Συνδυαστική.

Η προέλευση του ονόματος του παζλ είναι ασαφής, και έχει υποστηριχθεί ότι αυτό έχει ληφθεί από την αρχαία ελληνική λέξη για το λαιμό ή τον οισοφάγο, στόμαχος.^[60] Ο Αυσόνιος αναφέρεται στο παζλ, με την ονομασία "Οστομάχιον", μια ελληνική σύνθετη λέξη που σχηματίζεται από τις ρίζες του ὀστέον (οστό) και της μάχης (αγώνας). Το παζλ είναι επίσης γνωστό ως μικρό πακέτο (loculus) του Αρχιμήδη ή Κουτί του Αρχιμήδη.^[61]

• Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος (=μέθοδος)
  Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Η πραγματεία αυτή θεωρούνταν χαμένη μέχρι και την ανακάλυψη του Παλίμψηστου του Αρχιμήδη το 1906. Σε αυτό το έργο του, o Αρχιμήδης χρησιμοποιεί απειροστικά και δείχνει πώς η διαμέλιση ενός σχήματος σε έναν άπειρο αριθμό, απείρως μικρών κομματιών, μπορεί να μας βοηθήσει στο να προσδιορίσουμε το εμβαδόν ή και τον όγκο του. Ο Αρχιμήδης είχε υπόψη του πως αυτή η μέθοδος στερείται επίσημης αυστηρότητας, έτσι χρησιμοποίησε και τη μέθοδο της εξάντλησης για την εξαγωγή των αποτελεσμάτων. Όπως και το Πρόβλημα Βοοειδών, έτσι κι αυτό το έργο ήταν γραμμένο με τη μορφή επιστολής προς τον Ερατοσθένη, στην Αλεξάνδρεια.

• Περί των επιπλεόντων σωμάτων
  Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Στο πρώτο μέρος αυτής της πραγματείας, ο Αρχιμήδης εξηγεί το νόμο της ισορροπίας των υγρών κι αποδεικνύει πως το νερό θα υιοθετήσει μια σφαιρική μορφή γύρω από ένα κέντρο βαρύτητας. Αυτό μπορεί να ήταν μια προσπάθεια για να εξηγήσει τη θεωρία των τότε σύγχρονων Ελλήνων αστρονόμων, όπως και του Ερατοσθένη, ότι η Γη είναι σφαιρική. Τα υγρά περιγράφονται από τον Αρχιμήδη ως μη αυτο-βαρυτικά, δεδομένου ότι υποθέτει την ύπαρξη ενός σημείου, προς το οποίο εμπίπτουν όλα τα αντικείμενα, με αποτέλεσμα να αποκτούν το σφαιρικό τους σχήμα.

Στο δεύτερο μέρος, υπολογίζει τις θέσεις ισορροπίας διάφορων τμημάτων από παραβολοειδή. Αυτό ήταν ίσως μια εξιδανίκευση των σχημάτων, που δημιουργούσε το βυθισμένο μέρος των πλοίων στο νερό. Κάποια από αυτά τα τμήματα επιπλέουν με τη βάση κάτω από το νερό και τη μέγιστη (σε ύψος) κορυφή πάνω από το νερό, παρόμοια με τον τρόπο με τον οποίο τα παγόβουνα επιπλέουν. Η αρχή της άνωσης του Αρχιμήδη παρατίθεται σε αυτό το έργο, ως εξής:

«Κάθε σώμα που είναι εξ ολοκλήρου ή μερικώς βυθισμένο σε ένα ρευστό, δέχεται μια ώθηση ίση σε μέγεθος, αλλά αντίθετης φοράς, με το βάρος του εκτοπισμένου ρευστού.»

• Κατασκευή πλευράς του περιγραφομένου εις κύκλο επταγώνου
• Ωρολόγιον Αρχιμήδους (Σώζεται στα αραβικά)
• Περί κύκλων εφαπτομένων αλλήλων
• Αρχαί της Γεωμετρίας
• Οχουμένων (Υδροστατική επιπλεόντων σωμάτων)

Απόκρυφα έργα[Επεξεργασία | επεξεργασία κώδικα]

• Βιβλίο λημμάτων

Το έργο του Αρχιμήδη Βιβλίο λημμάτων ή Liber Assumptorum είναι μια πραγματεία με δεκαπέντε προτάσεις σχετικά με τη φύση των κύκλων. Το αρχαιότερο γνωστό αντίγραφο του κειμένου είναι στα αραβικά. Οι μελετητές T. L. Heath και Marshall Clagett υποστήριζαν πως δεν μπορεί να έχει γραφτεί από τον Αρχιμήδη, αυτό το έργο στη σημερινή του μορφή, δεδομένου ότι αναφέρει τον Αρχιμήδη σε τρίτο πρόσωπο, γεγονός που υποδηλώνει επεξεργασία από κάποιον άλλο συντάκτη. Το έργο αυτό μπορεί να βασίζεται σε μια προηγούμενη εργασία του Αρχιμήδη, η οποία πιθανότατα έχει χαθεί.^[62]

Επίσης, θεωρείται πως ο τύπος του Ήρωνα για τον υπολογισμό του εμβαδού ενός τριγώνου από το μήκος των πλευρών του, ήταν γνωστός στον Αρχιμήδη.^[c] Ωστόσο, η πρώτη αξιόπιστη αναφορά στον τύπο δίνεται από τον Ήρωνα τον Αλεξανδρεύς τον 1ο μ.Χ. αιώνα.^[63]

Μη διασωθέντα συγγράμματα
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

(ή συγγράμματα μη αποκαλυφθέντα μέχρι σήμερα)

• Αριθμητικά
• Βαρουλκός, Υδροσκοπίαι, Πνευματική
• Επισίδια Βιβλία (Μάλλον περί στατιστικής - Τζέτζης)
• Περί τριγώνων
• Περί τετραπλεύρου
• Περί ζευγών
• Περί 13 ημικανονικών πολυέδρων
• Ισοπεριμετικά
• Ισορροπίαι
• Καύσις δια κατόπτρων (επ΄ αυτού έγινε επιτυχές πείραμα στο Ν.Σ.)
• Περί Αρχιτεκτονικής
• Περί βαρύτητος και ελαφρότητος (Πυκνόμετρα - Αραιόμετρα)
• Περί δρομομέτρων (Οδόμετρα πλοίων)
• Περί κέντρου Βάρους ή Κεντροβαρικά
• Κατοπρικά
• Περί παραλλήλων γραμμών
• Περί κοίλων και παραβολικών κατόπτρων
• Προοπτική
• Στοιχεία μηχανικών
• Πλινθίδες και Κύλινδροι
• Στοιχεία επί των στηρίξεων
• Περί σφαιροποιΐας

Παλίμψηστο του Αρχιμήδη
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Το Οστομάχιο είναι ένα τεμαχισμένο παζλ που βρέθηκε στο Παλίμψηστο του Αρχιμήδη.

Κύριο λήμμα: Παλίμψηστο του Αρχιμήδη

Το κύριο έγγραφο που περιέχει το έργο του Αρχιμήδη είναι το Παλίμψηστο του Αρχιμήδη. Το 1906, ο Δανός καθηγητής Johan Ludvig Heiberg επισκέφθηκε την Κωνσταντινούπολη και εξέτασε περγαμηνή(από δέρμα κατσίκας), γραμμένη τον 13ο μ.Χ. αιώνα, η οποία περιείχε 174 σελίδες λειτουργικών κειμένων. Τελικά ανακάλυψε ότι η περγαμηνή ήταν ένα παλίμψηστο, δηλαδή ένα έγγραφο με κείμενο το οποίο είχε γραφεί πάνω σε μια σβησμένη παλιά εργασία. Τα παλίμψηστα δημιουργούνταν ξαίνοντας το μελάνι από τα αρχικά έργα των περγαμηνών και με την επαναχρησιμοποίηση τους. Αυτή ήταν μια συνηθισμένη πρακτική στον Μεσαίωνα, καθώς η περγαμηνή ήταν αρκετά ακριβή. Τα παλιότερα έργα στο παλίμψηστο αναγνωρίστηκαν από τους μελετητές τον 10ο αιώνα μ.Χ., ως αντίγραφα από προηγούμενες άγνωστες πραγματείες του Αρχιμήδη.^[64] Η περγαμηνή, πριν να πωληθεί σε ιδιώτη συλλέκτη το 1920, ήταν για εκατοντάδες χρόνια σε μια μοναστηριακή βιβλιοθήκη στην Κωνσταντινούπολη. Στις 29 Οκτωβρίου 1998, πωλήθηκε σε δημοπρασία σε έναν ανώνυμο αγοραστή για 2 εκατομμύρια δολάρια από τον οίκο Κρίστις, στη Νέα Υόρκη.^[65] Το παλίμψηστο περιέχει επτά πραγματείες, συμπεριλαμβανομένου και του μοναδικού σωζόμενου αντιγράφου του έργου "Περί των επιπλεόντων σωμάτων" στην αρχαία ελληνική. Είναι η μοναδική γνωστή πηγή του έργου "Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος", που αναφερότανε στη Σούδα και θεωρούνταν ότι είχε χαθεί για πάντα. Το "Οστομάχιον" επίσης ήταν στο παλίμψηστο, με μια πιο πλήρη ανάλυση του παζλ, σε σχέση με ό,τι είχε βρεθεί σε προηγούμενα κείμενα. Το παλίμψηστο είναι τώρα αποθηκευμένο στο Walters Art Museum της Βαλτιμόρης, Μέριλαντ, όπου υποβάλλεται σε διάφορων ειδών σύγχρονες δοκιμές, όπως η χρήση υπεριώδους ακτινοβολίας και ακτίνων Χ, έτσι ώστε να διαβαστεί το αρχικό κείμενο.^[66]

Οι πραγματείες του Αρχιμήδη στο Παλίμψηστο είναι: Περί επιπέδων ισορροπιών, Περί ελίκων, Κύκλου μέτρησις, Περί σφαίρας και κυλίνδρου, Περί των επιπλεόντων σωμάτων, Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος και Οστομάχιον.

Κληρονομιά
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Το Μετάλλιο Φιλντς φέρει το πορτρέτο του Αρχιμήδη.

• Υπάρχει ένας κρατήρας στη Σελήνη με το όνομα του Αρχιμήδη (29.7° Β, 4.0° Δ)προς τιμήν του, καθώς και μια σεληνιακή οροσειρά, ταβουνά του Αρχιμήδη (25.3° Β, 4.6° Δ).^[67]
• Ο αστεροειδής 3600 Αρχιμήδης πήρε το όνομά του από αυτόν.^[68]
• Το μετάλλιο Fields για εξαιρετικές επιδόσεις στα μαθηματικά φέρει ένα πορτρέτο του Αρχιμήδη, μαζί με ένα σκάλισμα απεικονίζει την απόδειξη του στη σφαίρα και τον κύλινδρο.Η επιγραφή γύρω από το κεφάλι του Αρχιμήδη είναι ένα απόσπασμα που αποδίδεται σ 'αυτόν,και γράφει στα λατινικά: "Transire suum pectus mundoque potiri" (Ανέβα πάνω από τον εαυτό σου και κατέκτησε τον κόσμο).^[69]
• Ο Αρχιμήδης έχει αποτυπωθεί στα γραμματόσημα που εκδίδονται από την Ανατολική Γερμανία (1973), Ελλάδα (1983), Ιταλία (1983), τηΝικαράγουα (1971), Σαν Μαρίνο (1982), και την Ισπανία (1963).^[70]
• Το επιφώνημα του Εύρηκα! που αποδίδεται στον Αρχιμήδη είναι το σύνθημα της πολιτείας της Καλιφόρνια.Στην περίπτωση αυτή η λέξη αναφέρεται στην ανακάλυψη του χρυσού κοντά στο Mill Sutter το 1848 που πυροδότησε την Καλιφορνιακή εξόρυξη χρυσού.^[71]
• Ένα κίνημα με πολιτική συμμετοχή,που αποσκοπεί στην καθολική πρόσβαση στην υγειονομική περίθαλψη στην αμερικανική πολιτεία του Όρεγκον έχει ονομαστεί το "Κίνημα Ο Αρχιμήδης», με επικεφαλής τον πρώην Κυβερνήτη του Όρεγκον John Kitzhaber.^[72]

Εφευρέσεις
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

"Αστρονομική συσκευή"

• "Βαρουλκός"
• "Γερανοί" (Αρπάγες)
• "Καταπέλτες"
• "Κάτοπτρα"
• "Κοχλίας ή έλιξ"
• "Οδόμετρο (δρομόμετρο)"
• "Πλανητάριον (σφαίρα)
• "Πολύσπαστον" (Βαρούλκο), "τρίσπαστο"
• "Σίφων"
• "Οστομάχιον" (επιτραπέζιο παιγνίδι το πρώτο παζλ)
• "Τηλεβόλον Αρχιμήδους"
• "Χαριστίων" (μοχλός)
• "Ωρολόγιο υδραυλικό"

Δείτε επίσης
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Παλίμψηστο του Αρχιμήδη Δρέπανος του Αρχιμήδη Αξίωμα του Αρχιμήδη Αρχή του Αρχιμήδη για την πλευστότητα

Στερεό του Αρχιμήδη Αρχύτας ο Ταραντίνος Διοκλής ο Αλεξανδρεύς

Τηλεβόλον Αρχιμήδους Συρακουσία Βιτρούβιος

Βιβλιογραφία
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

• Τάσιος, Θεοδόσιος Π.: «Το αντιτεχνοκρατικό σύνδρομο του Αρχιμήδη». Ελληνική Φιλοσοφική Επιθεώρηση 5 (1988), 174-181.
• Φίλη Χριστίνα, «Πυθαγόρας, Αρχιμήδης και ινδικές μαθηματικές θεωρίες», Φιλοσοφία 15-16 (1985-86), 156-171
• Σ.Α. Παϊπέτης - M. Ceccarelli (eds.), «The Genius of Archimedes». 23 Centuries of Influence on the Fields of Mathematics, Science, and Engineering. Proceedings of the International Symposium (Syracuse, 8-10/6/2010), Dordrecht, 2010.

Σημειώσεις
Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

a. ^{^}  Στο πρόλογο του Οι Σπείρες απευθυνόμενος στον Δοσίθεο από το Πηλούσιο, ο Αρχιμήδης λέει ότι "πολλά χρόνια πέρασαν από το θάνατο του Κόνωνα".Ο Κόνων ο Σάμιοςέζησε το 280-220π.Χ., υπονοώντας πως ο Αρχιμήδης ήταν μεγαλύτερης ηλικίας όταν έγραψε μερικά από τα έργα του.

b. ^{^}  Οι πραγματείες του Αρχιμήδη που γνωρίζουμε μέσα από έργα άλλων συγγραφέων είναι:Κατασκευές πάνω σε σφαίρα και μια εργασία πάνω στα πολύεδρα που την αναφέρει ο Πάππος ο Αλεξανδρινός· Κατοπτρικά, μια εργασία στην οπτική που αναφέρεται από τον Θέων τον Αλεξανδρεύς· Αρχές, όπου απευθύνεται στον Ζεύξιππο και του εξηγεί το αριθμητικό σύστημα που χρησιμοποιεί στα Ψαμμίτη· Ισσοροπίες και μοχλοί, Κέντρα βαρύτητας, Ημερολόγιο. Από τα επιζώντα έργα του Αρχιμήδη, ο T. L. Heath κάνει μια υπόθεση για τη σειρά με την οποία γραφτηκαν: Κέντρα βάρους επιπέδων I, Ο τετραγωνισμός της παραβολής, Κέντρα βάρους επιπέδων II, Περί σφαίρας και κυλίνδρου I, II, Οι Σπείρες, Περί σφαιροειδέων και κωνοειδέων, Περί επιπλεόντων σωμάτων I, II, Κύκλου μέτρησις, Ψαμμίτης.

c. ^{^} Καρλ Μπέντζαμιν Μπόγιερ A History of Mathematics(Μία Ιστορία Μαθηματικών) (1991) ISBN 0-471-54397-7 "'Αραβες μελετητές μας πληροφορούν, ότι ο γνωστός τύπος για τον υοπολογισμό του εμβαδού ενός τριγώνου,συναρτήσει των τριών πλευρών του(ευρέως γνωστός ως τύπος του 'Ηρωνα)  k = √(s(s − a)(s − b)(s − c)),όπου s η ημιπερίμετρος-ήταν γνωστός στον Αρχιμήδη αρκετούς αιώνες,πριν τη γέννηση του Ήρωνα.Επίσης,'Αραβες μελετητές αποδίδουν στον Αρχιμήδη το «θεώρημα για τη σπασμένη χορδή»....Ο Αρχιμήδης αναφέρεται από τους Άραβες πως έχει δώσει αρκετές αποδείξεις αυτού του θεωρήματος."

d. ^{^} "Ήταν σύνηθες να επιχρυσώνουν τις ραφές ή ακόμα και ολόκληρο το σκάφος με πίσσα ή με πίσσα και κερί". Στο έργο Νεκρικοὶ Διάλογοι, ο Λουκιανός αναφέρεται στην επικάλυψη των ραφών των σκιφ (είδος πλοίου) με κερί, μια αναφορά σε πίσσα ή κερί.^[73]

Νότα Κυμοθόη© Nota Kimothoi
Copyright:Νότα Κυμοθόη 

Αυτό το εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού-Μη Εμπορική Χρήση-Όχι Παράγωγα Έργα 4.0 Διεθνές .

Νότα Κυμοθόη "ΑΡΧΙΜΗΔΗΣ"Ιστορική έρευνα© Nότα Κυμοθόη